Simple Rating System
Motivation
In my last post, I was playing around with data from an API offered by http://collegefootballdata.com.
Then I found some blog posts on the site, and I thought a couple of them on how Simple Rating Systems work were interesting.
In particular, this one.
They did all their coding in Python, but I’m becoming more and more of an R fan, so I thought I’d re-code the wheel, so to speak.
In their post, they used data from the 2019 season, so for consistency, I’ll do the same.
Also, in the last post, I was using tidyr to un-nest JSON data.
It seemed add to me that you have to do these repeated unnest_auto() steps to get things parsed out.
If it’s automatic, why do I have to keep doing it manually?
After some more Googling, I found the tidyjson package, which has a nice spread_all function that I’ll use instead.
Simple Rating System: The Math
This, to me, is the coolest part.
I had no idea this is how some rating systems work, and it’s pretty slick.
It’s just one big system of equations that you solve with regular ‘ol linear algebra.
In other words, solve .
That’s it.
I’ll start with the b vector - that’s easiest to explain.
The b Vector
The b vector is each team’s average margin of victory for the season.
Couldn’t be any simpler.
The A Matrix
This is a little more complicated.
The A matrix will have dimensions of 130x130 - one row and column for each FBS team.
The diagonal will be 1’s (i.e., the identity matrix).
Think of the rest of the matrix in terms of rows.
We’ll set it up alphabetically, so the first row will be for Air Force.
First, we’ll count how many games Air Force played that season.
Then we’ll identify all of Air Force’s opponents - those are the columns.
As I said, the Air Force-Air Force entry will have a 1.
Moving across the columns, if Air Force didn’t play that team, put a 0 there.
If they did, divide the number of times Air Force played that team by the total number of games played and put that value in the column.
Keep doing that until you get to the last column (i.e., that last potential match-up).
Then repeat that process for the next team, Akron, and then the next, etc.
That’s it.
This matrix represents each team’s strength of schedule.
Pretty clever, right?
A teams rating is it’s mean margin of victory adjusted by it’s strength of schedule.
The Code
First we need to get all the FBS team names so we can exclude non-FBS games.
library(tidyjson)
library(dplyr)
library(httr)
fbs <-
httr::GET(
url = "https://api.collegefootballdata.com/teams/fbs?year=2019",
httr::add_headers(
Authorization = paste("Bearer", Sys.getenv("YOUR_API_TOKEN"))
)
)
fbs_teams <-
httr::content(fbs, "parsed") %>% # convert response to a nested list
spread_all %>% # rectangularize nested list into a dataframe
arrange(school) # make sure teams are in alphabetical order
Now we’ll get team win-loss records.
records <-
httr::GET(
url = "https://api.collegefootballdata.com/games?year=2019",
httr::add_headers(
accept = "application/json",
Authorization = paste("Bearer", Sys.getenv("YOUR_API_TOKEN"))
)
)
team_records <-
httr::content(records, "parsed") %>%
spread_all
Now get scores and margin of victory for each game and eliminate non-FBS games.
Eventually we’ll use this for the $b$ vector, but first we’ll need it in this format for the A matrix.
scores <- team_records %>%
filter(home_team %in% (fbs_teams %>% .$school) & away_team %in% (fbs_teams %>% .$school)) %>%
select(home_team, away_team, home_points, away_points) %>%
mutate(home_mov = home_points - away_points)
head(scores)
## # A tbl_json: 6 x 6 tibble with a "JSON" attribute
## ..JSON home_team away_team home_points away_points home_mov
## <chr> <chr> <chr> <dbl> <dbl> <dbl>
## 1 "{\"id\":401110723..." Florida Miami 24 20 4
## 2 "{\"id\":401114164..." Hawai'i Arizona 45 38 7
## 3 "{\"id\":401117854..." Cincinnati UCLA 24 14 10
## 4 "{\"id\":401111653..." Clemson Georgia Te~ 52 14 38
## 5 "{\"id\":401114236..." Tulane Florida In~ 42 14 28
## 6 "{\"id\":401110731..." Texas A&M Texas State 41 7 34
Ok, now we can start to generate the A matrix.
First, I’ll populate it with the number of times each team faced each other.
There’s probably a more elegant way, but this is what came to me first.
A <- data.frame(diag(0, nrow=130, ncol=130), row.names = fbs_teams %>% .$school)
colnames(A) <- fbs_teams %>% .$school
# populate dataframe with
for (r in 1:nrow(scores)){
home <- scores[r, 1] %>% .$home_team
away <- scores[r, 2] %>% .$away_team
A[home, away] <- A[home, away] + 1
A[away, home] <- A[away, home] + 1
}
# clean up
rm(away, home, r)
A[1:6, 1:6]
## Air Force Akron Alabama Appalachian State Arizona
## Air Force 0 0 0 0 0
## Akron 0 0 0 0 0
## Alabama 0 0 0 0 0
## Appalachian State 0 0 0 0 0
## Arizona 0 0 0 0 0
## Arizona State 0 0 0 0 1
## Arizona State
## Air Force 0
## Akron 0
## Alabama 0
## Appalachian State 0
## Arizona 1
## Arizona State 0
Hold that thought on the A matrix - we need a little more work to proceed.
Next, rearrange the scores data to get one margin of victory score for each team and each game.
mov <- scores %>%
select(home_team, home_mov) %>%
rename(team = home_team, mov = home_mov) %>%
bind_rows(scores %>%
select(away_team, home_mov) %>%
rename(team = away_team, mov = home_mov) %>%
mutate(mov = -mov))
Now count the total number of games each team played.
n_games <- mov %>% count(team) %>% .$n
Multiply A’s columns by 1 / n_games.
MARGIN=1 specifies to sweep across columns.
A <- sweep(A, 1/n_games, MARGIN=1, FUN =`*`)
Finally, add the identity matrix and A is built.
A <- A + diag(1, nrow=130, ncol=130)
A[1:6, 1:6]
## Air Force Akron Alabama Appalachian State Arizona
## Air Force 1 0 0 0 0.00000000
## Akron 0 1 0 0 0.00000000
## Alabama 0 0 1 0 0.00000000
## Appalachian State 0 0 0 1 0.00000000
## Arizona 0 0 0 0 1.00000000
## Arizona State 0 0 0 0 0.09090909
## Arizona State
## Air Force 0.00000000
## Akron 0.00000000
## Alabama 0.00000000
## Appalachian State 0.00000000
## Arizona 0.09090909
## Arizona State 1.00000000
Now calculate the mean margin of victory for each team.
This is the $b$ vector for the system of equations.
b <-
mov %>%
group_by(team) %>%
summarize(mean_mov = mean(mov)) %>%
.$mean_mov
It took a while to build the system of equations, but solving it is a one-liner.
solve(A, b)
## Air Force Akron Alabama
## 12.17488262 -22.66408637 32.60720600
## Appalachian State Arizona Arizona State
## 21.80515687 -13.03736947 1.10205537
## Arkansas Arkansas State Army
## -24.46835876 -0.52637216 1.05006201
## Auburn Ball State Baylor
## 5.88613703 0.40799928 14.36295601
## Boise State Boston College Bowling Green
## 17.32564683 -2.78480549 -33.10414546
## Buffalo BYU California
## 10.20151104 0.46092289 -6.46928285
## Central Michigan Charlotte Cincinnati
## 10.31277888 -4.34284716 7.36008829
## Clemson Coastal Carolina Colorado
## 41.48627376 0.83014089 -11.45324149
## Colorado State Connecticut Duke
## -2.51297888 -22.92597291 -10.33694277
## East Carolina Eastern Michigan Florida
## -12.21872118 -2.75282448 12.69160016
## Florida Atlantic Florida International Florida State
## 8.62463543 1.37276246 -6.07744689
## Fresno State Georgia Georgia Southern
## 0.50823966 15.23789346 -1.56619791
## Georgia State Georgia Tech Hawai'i
## -2.53872623 -20.00376049 0.03002992
## Houston Illinois Indiana
## -11.22633847 5.83248366 6.84673009
## Iowa Iowa State Kansas
## 10.19598383 8.32429892 -17.55664637
## Kansas State Kent State Kentucky
## 9.86298135 -0.90629641 11.16790944
## Liberty Louisiana Louisiana Monroe
## 11.38026279 14.12089636 -10.96010135
## Louisiana Tech Louisville LSU
## 19.83837303 -11.11555104 24.61782878
## Marshall Maryland Memphis
## -4.53506310 -21.13126417 16.67762020
## Miami Miami (OH) Michigan
## 3.40729287 -9.17435086 9.40439559
## Michigan State Middle Tennessee Minnesota
## -2.84667123 -5.41633827 14.54830499
## Mississippi State Missouri Navy
## -10.04679640 5.12551526 14.51847575
## NC State Nebraska Nevada
## -10.13346295 -1.06634224 -10.70442169
## New Mexico New Mexico State North Carolina
## -18.96441796 -26.88151749 1.61200847
## North Texas Northern Illinois Northwestern
## -1.33040741 -5.75767308 -9.39415805
## Notre Dame Ohio Ohio State
## 21.22221810 10.59616933 36.35622851
## Oklahoma Oklahoma State Old Dominion
## 15.82512098 3.23809017 -14.57638255
## Ole Miss Oregon Oregon State
## -0.47404615 20.18886699 -6.91414098
## Penn State Pittsburgh Purdue
## 13.07833337 -4.24030653 -4.44792009
## Rice Rutgers San Diego State
## -7.94447288 -27.74865910 11.75886571
## San José State SMU South Alabama
## -0.51222213 14.52255973 -17.50751350
## South Carolina South Florida Southern Mississippi
## -20.16977658 -15.55091539 -3.01895055
## Stanford Syracuse TCU
## -10.41277836 -5.93538233 -1.45957680
## Temple Tennessee Texas
## 2.25488829 -4.03217697 1.54246752
## Texas A&M Texas State Texas Tech
## 0.24533392 -19.98074165 -2.56724537
## Toledo Troy Tulane
## -9.23735051 -1.27992009 -1.44073888
## Tulsa UAB UCF
## -9.98788905 7.89737667 22.70582261
## UCLA UMass UNLV
## -9.73407669 -28.89607277 -12.08819590
## USC UT San Antonio Utah
## 3.58662283 -18.39429259 20.89793643
## Utah State UTEP Vanderbilt
## -9.99000619 -13.81130518 -22.07917803
## Virginia Virginia Tech Wake Forest
## 1.72160891 8.58302730 1.14879646
## Washington Washington State West Virginia
## 8.68703548 7.56504382 -12.05131807
## Western Kentucky Western Michigan Wisconsin
## 11.04805953 10.09365243 11.70814611
## Wyoming
## 10.07670372
If you’re familiar with linear models in R, this bit of code does the same thing.
Don’t forget to include a -1 to drop the intercept term.
lm_A <- cbind(A, b)
coefficients(lm(b ~ . -1 , data=lm_A))
## `Air Force` Akron Alabama
## 12.17488262 -22.66408637 32.60720600
## `Appalachian State` Arizona `Arizona State`
## 21.80515687 -13.03736947 1.10205537
## Arkansas `Arkansas State` Army
## -24.46835876 -0.52637216 1.05006201
## Auburn `Ball State` Baylor
## 5.88613703 0.40799928 14.36295601
## `Boise State` `Boston College` `Bowling Green`
## 17.32564683 -2.78480549 -33.10414546
## Buffalo BYU California
## 10.20151104 0.46092289 -6.46928285
## `Central Michigan` Charlotte Cincinnati
## 10.31277888 -4.34284716 7.36008829
## Clemson `Coastal Carolina` Colorado
## 41.48627376 0.83014089 -11.45324149
## `Colorado State` Connecticut Duke
## -2.51297888 -22.92597291 -10.33694277
## `East Carolina` `Eastern Michigan` Florida
## -12.21872118 -2.75282448 12.69160016
## `Florida Atlantic` `Florida International` `Florida State`
## 8.62463543 1.37276246 -6.07744689
## `Fresno State` Georgia `Georgia Southern`
## 0.50823966 15.23789346 -1.56619791
## `Georgia State` `Georgia Tech` `Hawai'i`
## -2.53872623 -20.00376049 0.03002992
## Houston Illinois Indiana
## -11.22633847 5.83248366 6.84673009
## Iowa `Iowa State` Kansas
## 10.19598383 8.32429892 -17.55664637
## `Kansas State` `Kent State` Kentucky
## 9.86298135 -0.90629641 11.16790944
## Liberty Louisiana `Louisiana Monroe`
## 11.38026279 14.12089636 -10.96010135
## `Louisiana Tech` Louisville LSU
## 19.83837303 -11.11555104 24.61782878
## Marshall Maryland Memphis
## -4.53506310 -21.13126417 16.67762020
## Miami `Miami (OH)` Michigan
## 3.40729287 -9.17435086 9.40439559
## `Michigan State` `Middle Tennessee` Minnesota
## -2.84667123 -5.41633827 14.54830499
## `Mississippi State` Missouri Navy
## -10.04679640 5.12551526 14.51847575
## `NC State` Nebraska Nevada
## -10.13346295 -1.06634224 -10.70442169
## `New Mexico` `New Mexico State` `North Carolina`
## -18.96441796 -26.88151749 1.61200847
## `North Texas` `Northern Illinois` Northwestern
## -1.33040741 -5.75767308 -9.39415805
## `Notre Dame` Ohio `Ohio State`
## 21.22221810 10.59616933 36.35622851
## Oklahoma `Oklahoma State` `Old Dominion`
## 15.82512098 3.23809017 -14.57638255
## `Ole Miss` Oregon `Oregon State`
## -0.47404615 20.18886699 -6.91414098
## `Penn State` Pittsburgh Purdue
## 13.07833337 -4.24030653 -4.44792009
## Rice Rutgers `San Diego State`
## -7.94447288 -27.74865910 11.75886571
## `San José State` SMU `South Alabama`
## -0.51222213 14.52255973 -17.50751350
## `South Carolina` `South Florida` `Southern Mississippi`
## -20.16977658 -15.55091539 -3.01895055
## Stanford Syracuse TCU
## -10.41277836 -5.93538233 -1.45957680
## Temple Tennessee Texas
## 2.25488829 -4.03217697 1.54246752
## `Texas A&M` `Texas State` `Texas Tech`
## 0.24533392 -19.98074165 -2.56724537
## Toledo Troy Tulane
## -9.23735051 -1.27992009 -1.44073888
## Tulsa UAB UCF
## -9.98788905 7.89737667 22.70582261
## UCLA UMass UNLV
## -9.73407669 -28.89607277 -12.08819590
## USC `UT San Antonio` Utah
## 3.58662283 -18.39429259 20.89793643
## `Utah State` UTEP Vanderbilt
## -9.99000619 -13.81130518 -22.07917803
## Virginia `Virginia Tech` `Wake Forest`
## 1.72160891 8.58302730 1.14879646
## Washington `Washington State` `West Virginia`
## 8.68703548 7.56504382 -12.05131807
## `Western Kentucky` `Western Michigan` Wisconsin
## 11.04805953 10.09365243 11.70814611
## Wyoming
## 10.07670372
To visualize the ratings, let’s make a plot of the top 25.
library(ggplot2)
library(forcats)
srs <-
tibble(team = fbs_teams$school,
rating = solve(A, b),
color = fbs_teams$color)
top_25 <-
srs %>%
arrange(desc(rating)) %>%
slice(1:25)
ggplot() +
geom_col(data = top_25, aes(x = fct_reorder(team, rating), y = rating), fill = top_25$color) +
coord_flip() +
theme_bw() +
ylab("Rating") +
xlab("Team")
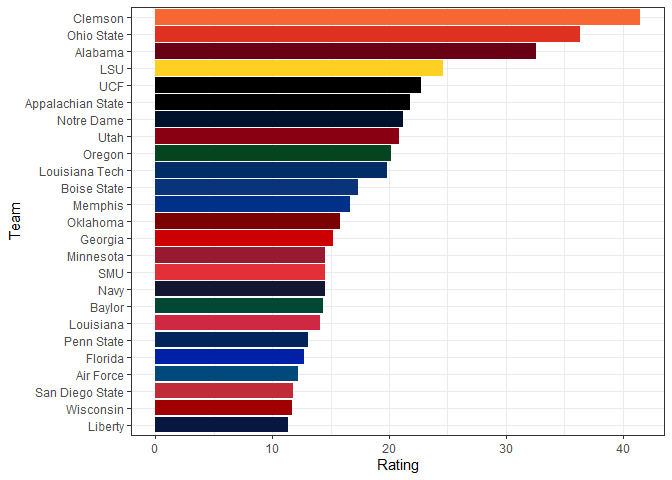
In the College Football Data blog, they further refine the rating by factoring in home field advantage, conference strength, and things like that.
That fine, but I just wanted to get the basic mechanics down.




Comments